2022-02-18 Householder QR
Contents
2022-02-18 Householder QR¶
Last time¶
Stability and ill conditioning
Intro to performance modeling
Classical vs Modified Gram-Schmidt
Today¶
Performance strategies
Right vs left-looking algorithms
Elementary reflectors
Householder QR
using LinearAlgebra
using Plots
using Polynomials
default(linewidth=4, legendfontsize=12)
function vander(x, k=nothing)
if isnothing(k)
k = length(x)
end
m = length(x)
V = ones(m, k)
for j in 2:k
V[:, j] = V[:, j-1] .* x
end
V
end
vander (generic function with 2 methods)
A Gram-Schmidt with more parallelism¶
(12)¶\[\begin{align}
(I - q_2 q_2^T) (I - q_1 q_1^T) v &= (I - q_1 q_1^T - q_2 q_2^T + q_2 q_2^T q_1 q_1^T) v \\
&= \Bigg( I - \Big[ q_1 \Big| q_2 \Big] \begin{bmatrix} q_1^T \\ q_2^T \end{bmatrix} \Bigg) v
\end{align}\]
function gram_schmidt_classical(A)
m, n = size(A)
Q = zeros(m, n)
R = zeros(n, n)
for j in 1:n
v = A[:,j]
R[1:j-1,j] = Q[:,1:j-1]' * v
v -= Q[:,1:j-1] * R[1:j-1,j]
R[j,j] = norm(v)
Q[:,j] = v / R[j,j]
end
Q, R
end
gram_schmidt_classical (generic function with 1 method)
m = 20
x = LinRange(-1, 1, m)
A = vander(x, m)
Q, R = gram_schmidt_classical(A)
@show norm(Q' * Q - I)
@show norm(Q * R - A)
norm(Q' * Q - I) = 1.4985231287367549
norm(Q * R - A) = 7.350692433565389e-16
7.350692433565389e-16
Why does order of operations matter?¶
(13)¶\[\begin{align}
(I - q_2 q_2^T) (I - q_1 q_1^T) v &= (I - q_1 q_1^T - q_2 q_2^T + q_2 q_2^T q_1 q_1^T) v \\
&= \Bigg( I - \Big[ q_1 \Big| q_2 \Big] \begin{bmatrix} q_1^T \\ q_2^T \end{bmatrix} \Bigg) v
\end{align}\]
is not exact in finite arithmetic.
We can look at the size of what’s left over¶
We project out the components of our vectors in the directions of each \(q_j\).
x = LinRange(-1, 1, 20)
A = vander(x)
Q, R = gram_schmidt_classical(A)
scatter(diag(R), yscale=:log10)
The next vector is almost linearly dependent¶
x = LinRange(-1, 1, 20)
A = vander(x)
Q, _ = gram_schmidt_classical(A)
#Q, _ = qr(A)
v = A[:,end]
@show norm(v)
scatter(abs.(Q[:,1:end-1]' * v), yscale=:log10)
norm(v) = 1.4245900685395503
Cost of Gram-Schmidt?¶
We’ll count flops (addition, multiplication, division*)
Inner product \(\sum_{i=1}^m x_i y_i\)?
Vector “axpy”: \(y_i = a x_i + y_i\), \(i \in [1, 2, \dotsc, m]\).
Look at the inner loop:
for k in 1:j-1
r = Q[:,k]' * v
v -= Q[:,k] * r
R[k,j] = r
end
Counting flops is a bad model¶
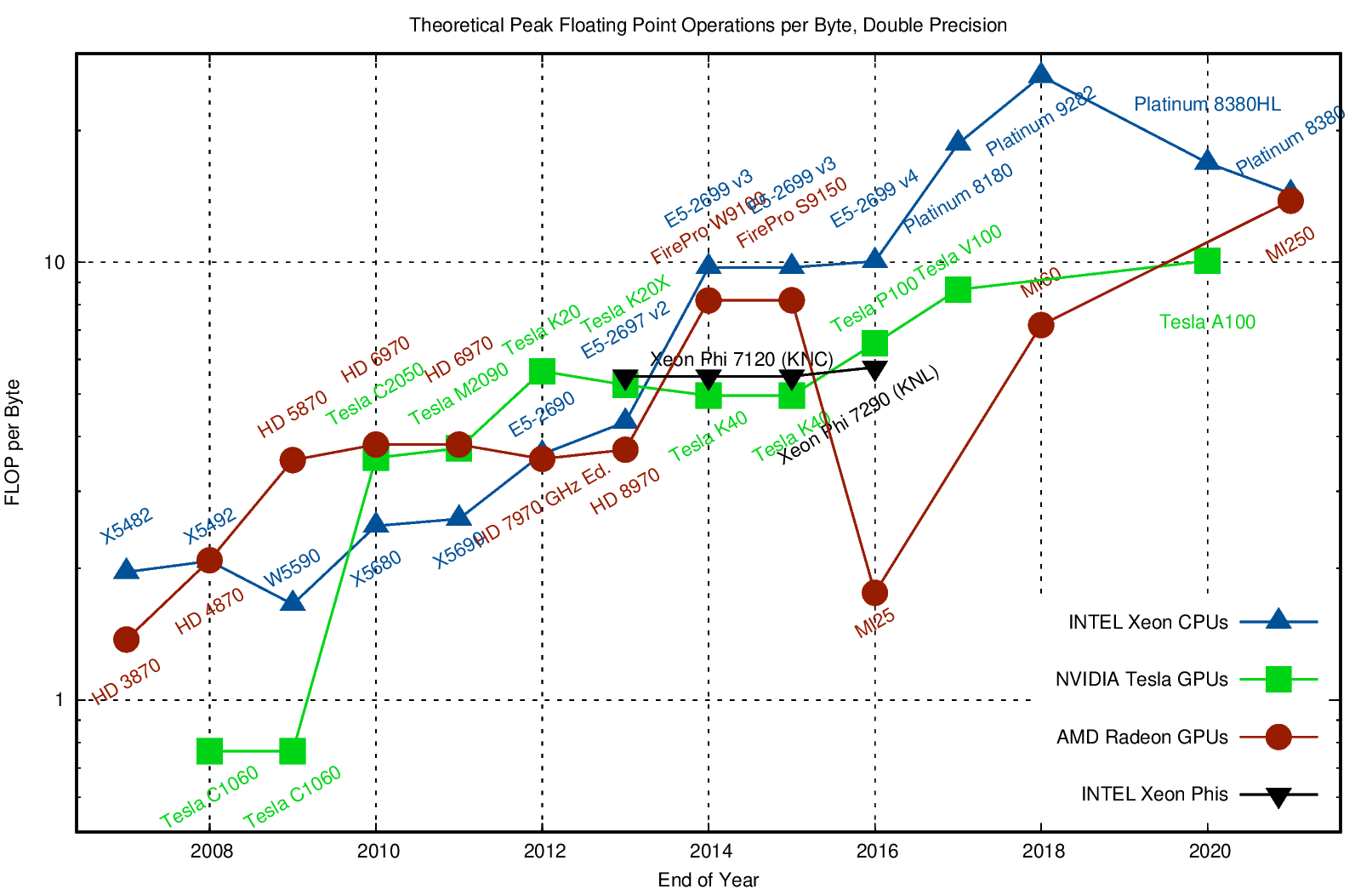
We load a single entry (8 bytes) and do 2 flops (add + multiply). That’s an arithmetic intensity of 0.25 flops/byte.
Current hardware can do about 10 flops per byte, so our best algorithms will run at about 2% efficiency.
Need to focus on memory bandwidth, not flops.
Inherent data dependencies¶
\[\begin{split} \Bigg[ q_1 \Bigg| q_2 \Bigg| q_3 \Bigg| q_4 \Bigg| q_5 \Bigg] \begin{bmatrix} r_{11} & r_{12} & r_{13} & r_{14} & r_{15} \\
& r_{22} & r_{23} & r_{24} & r_{25} \\
& & r_{33} & r_{34} & r_{35} \\
&&& r_{44} & r_{45} \\
&&& & r_{55}
\end{bmatrix}
\end{split}\]
Right-looking modified Gram-Schmidt¶
function gram_schmidt_modified(A)
m, n = size(A)
Q = copy(A)
R = zeros(n, n)
for j in 1:n
R[j,j] = norm(Q[:,j])
Q[:,j] /= R[j,j]
R[j,j+1:end] = Q[:,j]'*Q[:,j+1:end]
Q[:,j+1:end] -= Q[:,j]*R[j,j+1:end]'
end
Q, R
end
gram_schmidt_modified (generic function with 1 method)
m = 20
x = LinRange(-1, 1, m)
A = vander(x, m)
Q, R = gram_schmidt_modified(A)
@show norm(Q' * Q - I)
@show norm(Q * R - A)
norm(Q' * Q - I) = 8.486718528276085e-9
norm(Q * R - A) = 8.709998074379606e-16
8.709998074379606e-16
Classical versus modified?¶
Classical
Really unstable, orthogonality error of size \(1 \gg \epsilon_{\text{machine}}\)
Don’t need to know all the vectors in advance
Modified
Needs to be right-looking for efficiency
Less unstable, but orthogonality error \(10^{-9} \gg \epsilon_{\text{machine}}\)
m = 20
x = LinRange(-1, 1, m)
A = vander(x, m)
Q, R = qr(A)
@show norm(Q' * Q - I)
norm(Q' * Q - I) = 3.1195004131362406e-15
3.1195004131362406e-15
Householder QR¶
Gram-Schmidt constructed a triangular matrix \(R\) to orthogonalize \(A\) into \(Q\). Each step was a projector, which is a rank-deficient operation. Householder uses orthogonal transformations (reflectors) to triangularize.
\[ \underbrace{Q_{n} \dotsb Q_1}_{Q^T} A = R \]
The structure of the algorithm is
\[\begin{split} \underbrace{\begin{bmatrix} * & * & * \\ * & * & * \\ * & * & * \\ * & * & * \\ * & * & * \\ \end{bmatrix}}_{A} \to
\underbrace{\begin{bmatrix} * & * & * \\ 0 & * & * \\ 0 & * & * \\ 0 & * & * \\ 0 & * & * \\ \end{bmatrix}}_{Q_1 A} \to
\underbrace{\begin{bmatrix} * & * & * \\ 0 & * & * \\ 0 & 0 & * \\ 0 & 0 & * \\ 0 & 0 & * \\ \end{bmatrix}}_{Q_2 Q_1 A} \to
\underbrace{\begin{bmatrix} * & * & * \\ 0 & * & * \\ 0 & 0 & * \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}}_{Q_3 Q_2 Q_1 A}
\end{split}\]
Constructing the \(Q_j\)¶
\[ \underbrace{Q_{n} \dotsb Q_1}_{Q^T} A = R \]
Each of our \(Q_j\) will have the form
\[\begin{split}Q_j = \begin{bmatrix} I_i & 0 \\ 0 & F \end{bmatrix}\end{split}\]
where \(F\) is a “reflection” that achieves
\[\begin{split} F x = \begin{bmatrix} \lVert x \rVert \\ 0 \\ 0 \\ \vdots \end{bmatrix} \end{split}\]
where \(x\) is the column of \(R\) from the diagonal down.
This transformation is a reflection across a plane with normal \(v = Fx - x = \lVert x \rVert e_1 - x\).
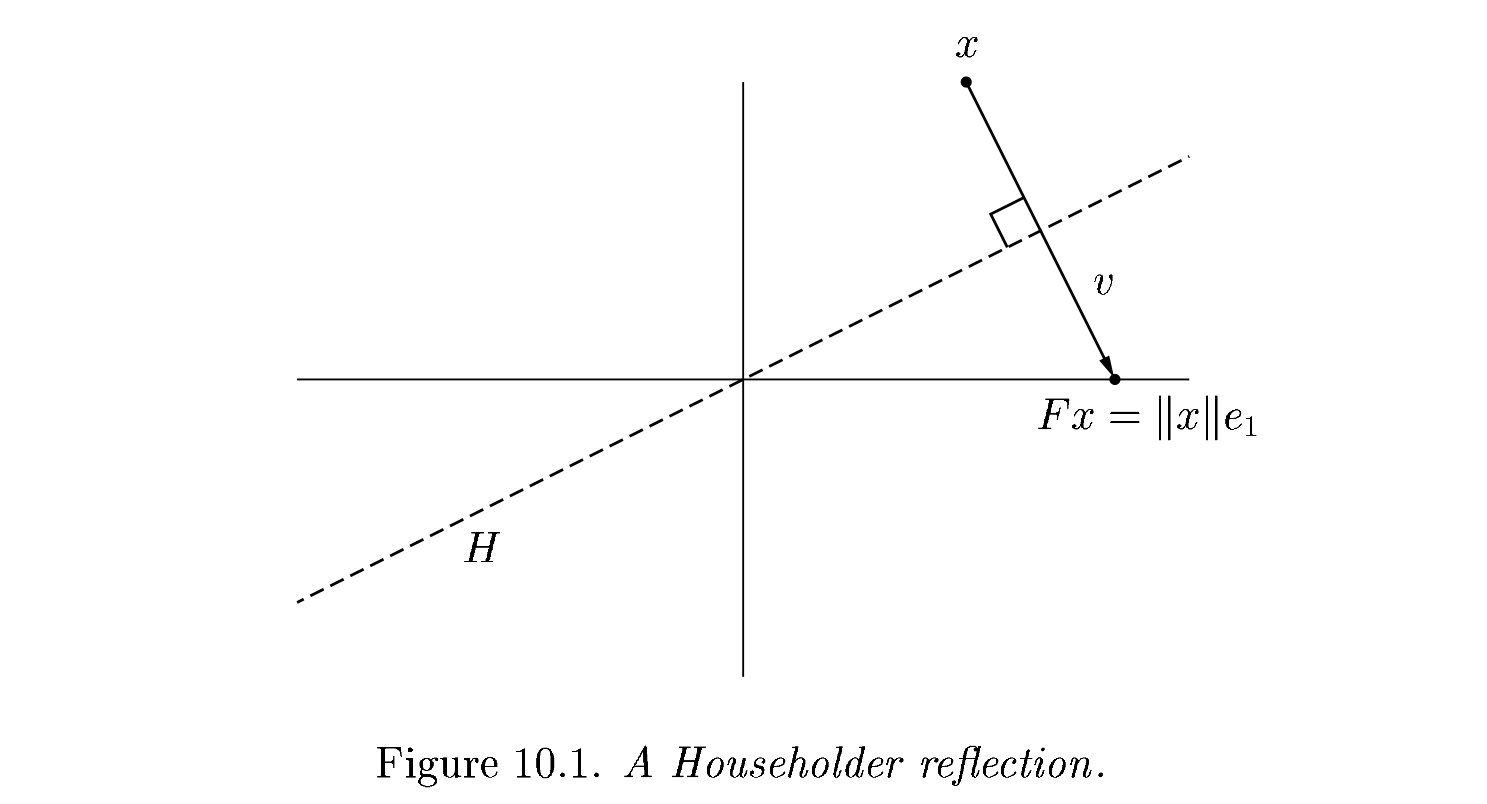
The reflection, as depicted above by Trefethen and Bau (1999) can be written \(F = I - 2 \frac{v v^T}{v^T v}\).
Adventures in reflection¶
A = rand(4, 4); A += A'
v = copy(A[:,1])
v[1] -= norm(v)
v = normalize(v)
F = I - 2 * v * v'
B = F * A
4×4 Matrix{Float64}:
2.1741 1.25714 0.99767 1.18672
-6.55398e-16 0.118113 0.765884 1.28508
-2.96172e-16 1.05277 -0.0743418 0.52617
-8.46837e-16 0.985914 0.0179292 0.779973
v = copy(B[2:end, 2])
v[1] -= norm(v); v = normalize(v)
F = I - 2 * v * v'
B[2:end, 2:end] = F * B[2:end, 2:end]
B
4×4 Matrix{Float64}:
2.1741 1.25714 0.99767 1.18672
-6.55398e-16 1.44717 0.020642 1.01903
-2.96172e-16 0.0 0.515979 0.736919
-8.46837e-16 1.11022e-16 0.570759 0.977337
An algorithm¶
function qr_householder_naive(A)
m, n = size(A)
R = copy(A)
V = [] # list of reflectors
for j in 1:n
v = copy(R[j:end, j])
v[1] -= norm(v)
v = normalize(v)
R[j:end,j:end] -= 2 * v * (v' * R[j:end,j:end])
push!(V, v)
end
V, R
end
qr_householder_naive (generic function with 1 method)
m = 4
x = LinRange(-1, 1, m)
A = vander(x, m)
V, R = qr_householder_naive(A)
_, R_ = qr(A)
R_
4×4 Matrix{Float64}:
-2.0 0.0 -1.11111 0.0
0.0 1.49071 1.38778e-17 1.3582
0.0 0.0 0.888889 9.71445e-17
0.0 0.0 0.0 0.397523
How to interpret \(V\) as \(Q\)?¶
function reflectors_mult(V, x)
y = copy(x)
for v in reverse(V)
n = length(v) - 1
y[end-n:end] -= 2 * v * (v' * y[end-n:end])
end
y
end
function reflectors_to_dense(V)
m = length(V[1])
Q = diagm(ones(m))
for j in 1:m
Q[:,j] = reflectors_mult(V, Q[:,j])
end
Q
end
reflectors_to_dense (generic function with 1 method)
m = 20
x = LinRange(-1, 1, m)
A = vander(x, m)
V, R = qr_householder_naive(A)
Q = reflectors_to_dense(V)
@show norm(Q' * Q - I)
@show norm(Q * R - A);
norm(Q' * Q - I) = 3.7994490775439526e-15
norm(Q * R - A) = 7.562760794606217e-15
Great, but we can still break it¶
A = [1 0; 0 1.]
V, R = qr_householder_naive(A)
(Any[[NaN, NaN], [NaN]], [NaN NaN; NaN NaN])
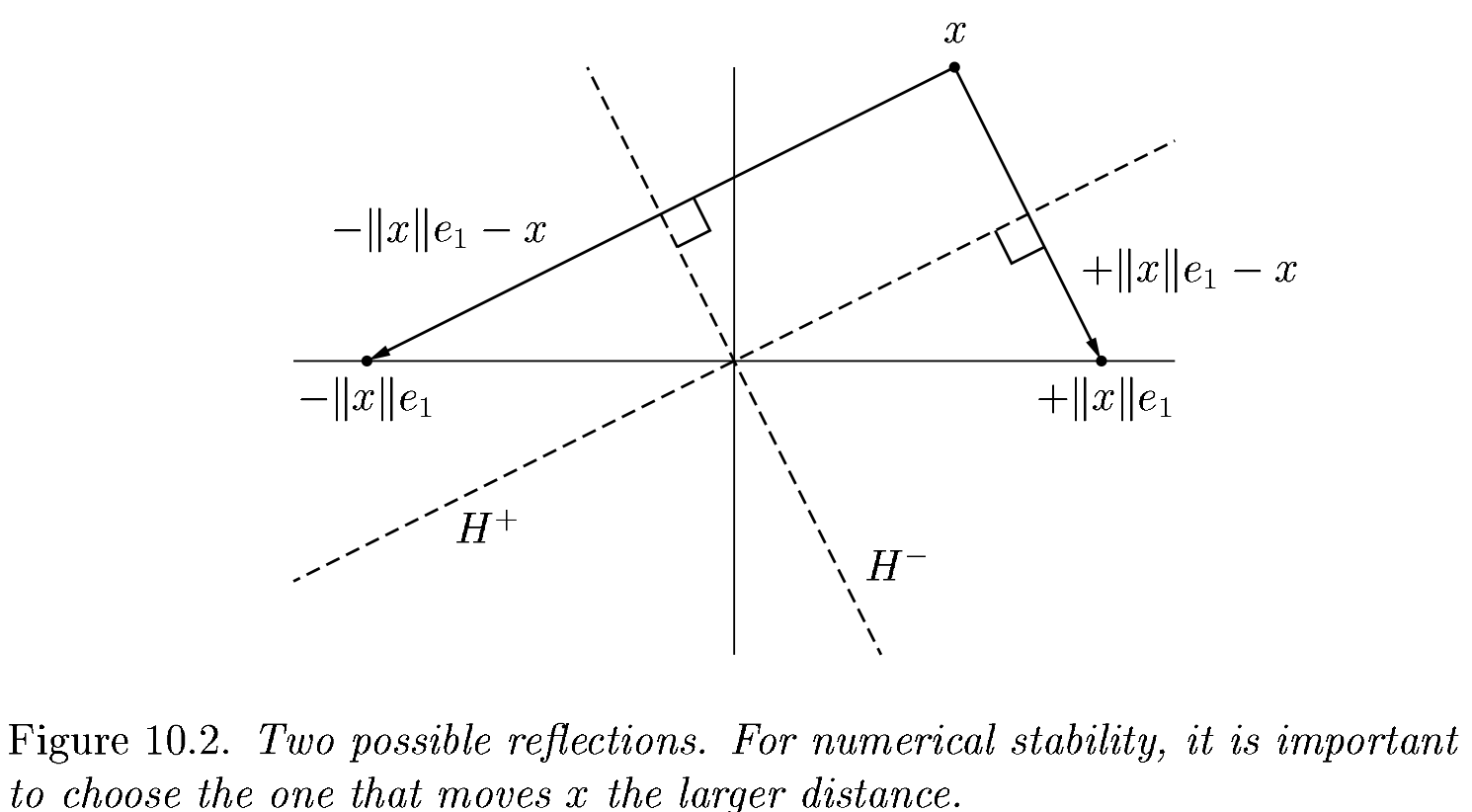
We had the lines
v = copy(R[j:end, j])
v[1] -= norm(v)
v = normalize(v)
What happens when R is already upper triangular?
An improved algorithm¶
function qr_householder(A)
m, n = size(A)
R = copy(A)
V = [] # list of reflectors
for j in 1:n
v = copy(R[j:end, j])
v[1] += sign(v[1]) * norm(v) # <---
v = normalize(v)
R[j:end,j:end] -= 2 * v * v' * R[j:end,j:end]
push!(V, v)
end
V, R
end
qr_householder (generic function with 1 method)
A = [2 -1; -1 2] * 1e-10
V, R = qr_householder(A)
tau = [2*v[1]^2 for v in V]
@show tau
V1 = [v ./ v[1] for v in V]
@show V1
R
tau = [1.894427190999916, 2.0]
V1 = [[1.0, -0.2360679774997897], [1.0]]
2×2 Matrix{Float64}:
-2.23607e-10 1.78885e-10
-1.29247e-26 -1.34164e-10
Householder is backward stable¶
m = 40
x = LinRange(-1, 1, m)
A = vander(x, m)
V, R = qr_householder(A)
Q = reflectors_to_dense(V)
@show norm(Q' * Q - I)
@show norm(Q * R - A);
norm(Q' * Q - I) = 5.949301496893686e-15
norm(Q * R - A) = 1.2090264267288813e-14
A = [1 0; 0 1.]
V, R = qr_householder(A)
qr(A)
LinearAlgebra.QRCompactWY{Float64, Matrix{Float64}}
Q factor:
2×2 LinearAlgebra.QRCompactWYQ{Float64, Matrix{Float64}}:
1.0 0.0
0.0 1.0
R factor:
2×2 Matrix{Float64}:
1.0 0.0
0.0 1.0
Orthogonality is preserved¶
x = LinRange(-1, 1, 20)
A = vander(x)
Q, _ = gram_schmidt_classical(A)
v = A[:,end]
@show norm(v)
scatter(abs.(Q[:,1:end-1]' * v), yscale=:log10, title="Classical Gram-Schmidt")
norm(v) = 1.4245900685395503
Q = reflectors_to_dense(qr_householder(A)[1])
scatter(abs.(Q[:,1:end-1]' * v), yscale=:log10, title="Householder QR")
