2022-01-10 First Day

2022-01-10 First Day¶

CSCI-3656: Numerical Computation¶

Instructor: Jed Brown, jed.brown@colorado.edu, ECOT 824¶

Meeting: Mon, Wed, Fri at 1:25-2:15 in FLMG 157 (and virtually)¶

Who am I?
What is this course about?
How will it work?
Discussion
(maybe) First activity

Who am I?¶

Jed Brown (he/him); you can call me Jed
Math + Physics undergrad, MS Math, Dr.Sc. Environmental Engineering (Computational Glaciology)
Postdoc and staff at Argonne National Laboratory (DOE Office of Science)
CU since 2015

Physical Prediction, Inference, and Design Group¶

Develop and maintain open source libraries
Research in fast/parallel algorithms, extensible software
Partner with scientists and engineers in many disciplines: geoscience, aerospace, civil engineering, fusion
Listen, learn about computational bottlenecks, build technology and communities

Prerequisites¶

Calculus¶

Fundamental Theorem of Calculus
Differentiate and integrate polynomials
Taylor series
Gradients (we’ll introduce and discuss)

We won’t use integral tricks (and any time you spent on that was a waste; sorry)

Linear Algebra¶

vector spaces, orthogonality
QR factorization
projectors, reflectors, and rotations (will teach)

We’ll never compute RREF or eigenvalues by hand (and any time you spent on that was a waste; sorry)

What is Numerical Computation?¶

From Trefethen (1992)

Here is the wrong answer:

Numerical analysis is the study of rounding errors.

Trefethen goes on to propose

Numerical analysis is the study of algorithms for the problems of continuous mathematics.

Continuous mathematics¶

real and complex numbers \(a \in \mathbb R\)
vectors \(\mathbf x \in \mathbb R^n\)
matrices \(A \in \mathbb R^{m\times n}\)
functions \(f: \mathbb R \to \mathbb R\)
higher order functions: \(g(f)\)

Finite vs Infinite algorithms¶

Compute the matrix product \(A B\)
Solve \(A x = b\) for \(x\)
Compute the eigenvalues \(\lambda\) of \(A \in \mathbb R^{10\times 10}\)
Compute \(\int_a^b f(x)\)

Rootfinding¶

Given \(f(x)\), find \(x\) such that \(f(x) = 0\).

Cost
- Evaluation of \(f(x)\) and perhaps derivatives \(f'(x)\).
- Other arithmetic
Convergence: how many evaluations to reach a given accuracy?
Robustness: does the algorithm always converge?

using Plots
default(linewidth=3)

f(x) = exp(x) * cos(x) + 1
plot([f, x -> 0], xlims=[-2.5, 5])

../_images/2022-01-10-first-day_12_0.svg

Numerical linear algebra¶

Finite algorithms for factorization¶

\(QR = A\), such that \(Q^T Q = I\) and \(R\) is right-triangular.
\(L U = A\), such that \(L\) and \(U\) are lower and upper triangular, respectively.

Infinite (iterative) algorithms¶

\(X \Lambda X^{-1} = A\) where \(\Lambda\) is diagonal.
\(U \Sigma V^T = A\), such that \(U^T U = I\), \(V^T V = I\), and \(\Sigma\) is diagonal with nonnegative entries.
Iterative solution of \(Ax=b\) using Krylov basis \(\{b, Ab, A^2b, \dotsc \}\)

Concepts¶

Accurate estimates of cost
Orthogonality, null spaces, projections
Geometry and modeling
Stable and backwards-stable algorithms
Conditioning
Develop a language in which to frame many concepts in the course

Approximating functions from data¶

Interpolation¶

Given samples \((x_0, f(x_0)), (x_1, f(x_1)), \dotsc\), determine an easily-computable function \(g(x)\) that exactly fits these samples and behaves sensibly in between.

Regression¶

Given noisy data \((x_0, y_0), (x_1, y_1), \dotsc\), determine an easily-computable function \(g(x)\) that explains these data.

We will need to make subjective choices to specify a problem with a unique solution.

Calculus: functions of functions¶

Differentiation¶

Given a function \(f(x)\) (as a computer program or callable function), define a new function

\[g(x) \approx f'(x). \]

We can do this

Numerically (black box)
By-hand code transformation
Automatic code transformation

Integration¶

Given a function \(f(x)\) (as a computer program or callable function), approximate the integral

\[ \int_a^b f(x) . \]

Numerical optimization¶

Given a scalar function \(f(x)\) (and perhaps its gradient \(f'(x)\)), determine

\[ x_* = \operatorname{argmin}_x f(x) . \]

Differential equations¶

Given a dynamical system

\[ \frac{\partial u(t)}{\partial t} = f(u(t)), \]

and initial condition \(u(0) = u_0\), estimate \(u(t)\) for arbitrary \(t\).

Higher dimensions¶

Many of these algorithms will generalize to functions of multiple variables. Different algorithms may be needed for such “high-dimensional” problems.

Computer Science = Runnable Abstraction Science¶

In the “grinder”¶

Mathematical language and principles for each major class of method
- What is covered by theory
- When you’re venturing off-trail
- Analytic tools to predict and debug
Realistic cost and exploitable structure
- Performance on modern hardware
Write/modify stand-alone code
Select and use (parallel) libraries

How can you trust the solution?¶

Verification: solving the problem right
Validation: solving the right problem

Abstractions/collaboration¶

Domain scientists, engineers
Optimizers, statisticians
Abstractions that reduce cognitive load
Metrics/visualization for decisions

On programming languages¶

C¶

Reliable and popular for libraries (PETSc, etc.). “Simple”, unsafe, capable of encapsulation.

C++¶

Popular with applications and some libraries. Powerful, but complicated and unsafe.

Fortran¶

The OG of numerical computing. Good for “array programming”, but encapsulation is hard. Unsafe depending on dialect.

Julia¶

For ground-up examples in class and in activities. Capable of high performance, expressive multiple dispatch, works well in a notebook. Error messages are not great.

Python¶

Good access to JIT, though with sharp edges. Poor native performance, but good libraries to compiled code.

Rust¶

New compiled language. Good performance, encapsulation, safety, static analysis. Poor libraries (so far).

You don’t need to know any of these well and you can choose the language for your project.

I won’t grade and I won’t waste your time¶

I will provide feedback

I will be a mentor and guide navigating this field

I will help you get what you want out of the class (with a dash of wholesome context)

My mom said, “basically, your professor is asking you to be an adult”. That was too flexible.

In other classes, I didn’t feel like I could bounce back, but in this one I did.

What about the letter grade?¶

Collect a portfolio of the work and insights you’re most proud of
Individual meetings during the last week of the semester (mid-term preview)
We’ll have a conversation and you’ll propose a grade based on your portfolio
- I’ll trust you.

I can nudge upward when students are too modest – pretty common. In rare cases, I may adjust down.

What I need from you: Growth Mindset¶

How will the semester look?¶

Lecture periods¶

Refresh, introduce, activity/group discussion, reflect
Pointers to further resources/activities

In-class and homework activities¶

(Short) coding, experiments, presentation of results
Use the math and programming tools of the field
Open-ended, go further occasionally

Learning plans¶

Write, track, and revise a personal learning plan.
Meet/chat approx weekly to check in with partner

Projects (second half of semester)¶

Dig into community software that implements or relies on numerical computation
Short presentation on how the community works
Key stakeholders
Strengths and weaknesses
Discuss and critique

Original study or contribution¶

Tutorial, documentation, performance study, comparison, new features, new application
Reflect in a short presentation

Expectations¶

Attend class (in-person or virtual) and participate in discussions
Make an honest attempt on activities
Interact with the class notebooks and read reference material
Set goals and track your progress

revise these goals as you learn more

Meet/chat with your partner weekly for at least a few minutes

share how lecture and activities are going
share your goals and how you’re progressing
identify questions

Ask or answer at least one question per week

ask a question that you don’t know the answer to
ask a question that you do know the answer to, but you think will be a good exercise/seed for discussion
ask me during office hours, write up your best understanding
make a meme relevant to the class
raise a concern or suggestion that you and/or peers have
contribute an answer or relevant discussion to any of the above

Individual and group projects

Tools¶

Git and GitHub¶

GitHub Classroom to manage repositories
Write using notebooks and markdown
Review using GitHub tools and nbgrader

Zulip¶

math- and code-aware team chat
live, informal
thread managemnet so a question in class can spin off into a deeper asynchronous conversation

Jupyter¶

RISE slides available on website
Activities with scaffolding
Nbgrader for writing feedback
Works with many languages; we’ll mostly use Julia
Collaborative mode (new)

JupyterHub: coding.csel.io ¶

Nothing to install, persistent storage
Select CSCI-3656 tile

A note about COVID¶

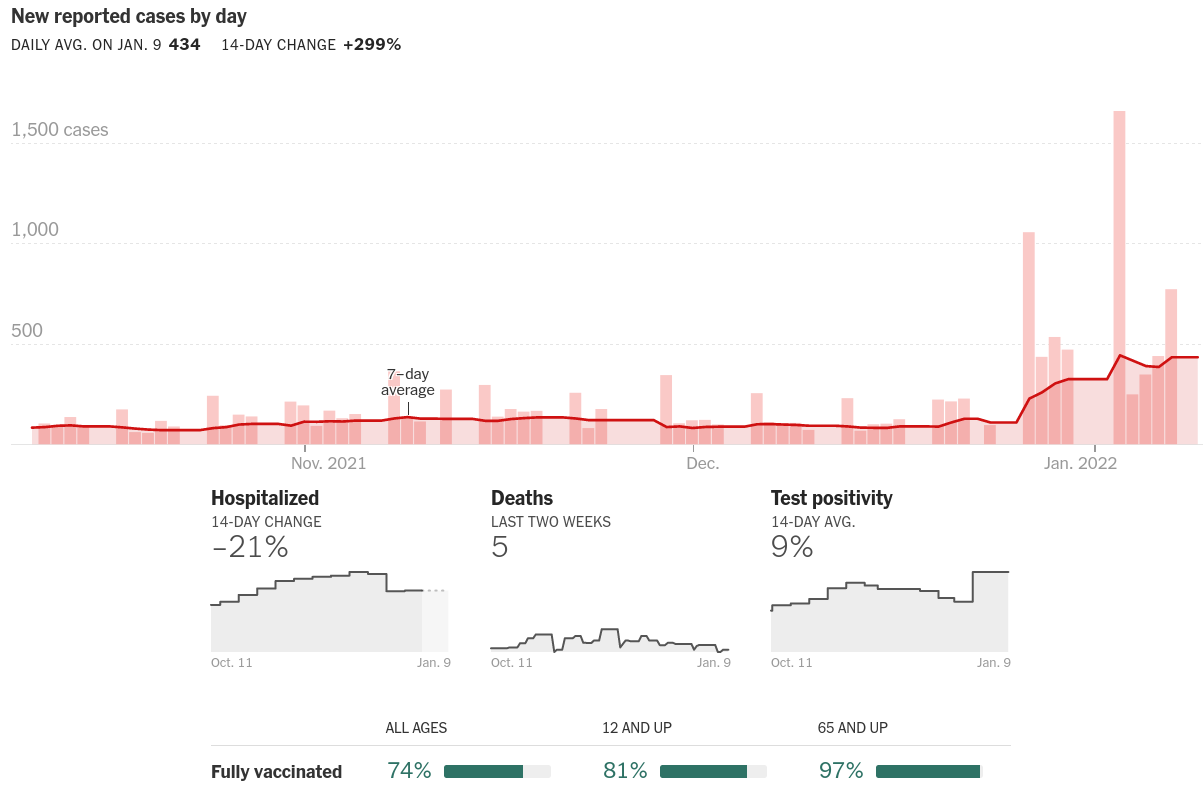
Boulder County cases are high and increasing
Breakthrough cases are very common with Omicron
I have a 1yo and 4yo in childcare
Pediatric hospitals are overwhelmed
They need to stay home and be tested any time they have symptoms

I’d prefer to do virtual office hours until 7-day average new cases drops below 30/day or my child can be vaccinated.
I’ll likely be home with a kid and need to teach remotely or otherwise make it up to you

Poll: What is floating point arithmetic?¶

fuzzy arithmetic
exact arithmetic, correctly rounded
the primary focus of numerical analysis

0.1 + 0.2

0.30000000000000004

plot(x -> 1 + x)

../_images/2022-01-10-first-day_56_0.svg

Machine epsilon¶

We approximate real numbers with floating point arithmetic, which can only represent discrete values. In particular, there exists a largest number, which we call \(\epsilon_{\text{machine}}\), such that

\[ 1 \oplus x = 1 \quad \text{for all}\ \lvert x \rvert < \epsilon_{\text{machine}}.\]

The notation \(\oplus, \ominus, \odot, \oslash\) represent the elementary operation carried out in floating point arithmetic.

eps = 1
while 1 + eps != 1
    eps = eps / 2
end
eps

1.1102230246251565e-16

Beating `exp`¶

\[e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dotsb\]

Suppose we want to compute \(f(x) = e^x - 1\) for small values of \(x\).

f1(x) = exp(x) - 1
y1 = f1(1e-8)

9.99999993922529e-9

f2(x) = x + x^2/2 + x^3/6
y2 = f2(1e-8)

1.000000005e-8

Which answer is more accurate?

@show (y1 - y2)        # Absolute difference
@show (y1 - y2) / y2;  # Relative difference

y1 - y2 = -1.1077470910720506e-16
(y1 - y2) / y2 = -1.1077470855333152e-8

Slides

2022-01-12 Functions

Numerical Computation